前言

很快啊，今天的第二篇，完整代码见 https://github.com/zong4/AILearning。

Reinforcement Learning

终于来到我最喜欢的强化学习了。

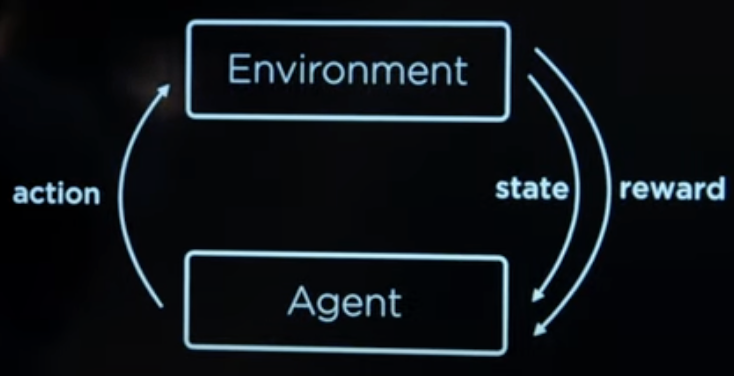
强化学习中各要素的关系如图所示。

  • 环境会告诉代理目前的状态，由此可以推出代理可以作出的行动。
  • 代理根据自己的判断选择行动后，环境会给出相应的惩罚或者奖励。
  • 不断循环上面两步直到代理成功或者失败。
  • 继续训练，不断的开始下一局游戏

OK，那接下来我们就来看个例子吧。

尼姆（取物）游戏

给大家看一眼应该大家就知道怎么玩了，我这里的话是谁最后取完谁输。

小潮院长他们最新一期羊村也玩了。

Agent

这里用的学习算法是 Q-learning，公式如下。

$$Q(s, a) <- Q(s, a) + alpha * (new_value_estimate - old_value_estimate)$$

其中 alpha 是学习率，new_value_estimate = reward（现阶段的奖励）+ best_future_reward（未来最大的奖励）。

具体实现主要是下面的 update(self, old_state, action, new_state, reward)。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
class NimAI():
    def __init__(self, alpha=0.5, epsilon=0.1):
        self.q = dict()
        self.alpha = alpha
        self.epsilon = epsilon

    def update(self, old_state, action, new_state, reward):
        old = self.get_q_value(old_state, action)
        best_future = self.best_future_reward(new_state)
        self.update_q_value(old_state, action, old, reward, best_future)

    def get_q_value(self, state, action):
        return self.q.get((tuple(state), action), 0)

    def update_q_value(self, state, action, old_q, reward, future_rewards):
        self.q[(tuple(state), action)] = old_q + self.alpha * (reward + future_rewards - old_q)

    def best_future_reward(self, state):
        if not Nim.available_actions(state):
            return 0
        return max([self.get_q_value(state, action) for action in Nim.available_actions(state)])

    def choose_action(self, state, epsilon=True):
        # Return best action
        if epsilon:
            if random.random() < self.epsilon:
                return random.choice(list(Nim.available_actions(state)))
        
        best_action = None
        best_q = float('-inf')
        for action in Nim.available_actions(state):
            q = self.get_q_value(state, action)
            if q > best_q:
                best_q = q
                best_action = action
        return best_action

训练

训练的代码如下，这里只需要最后一步有给奖励，诶，这就是算法神奇的地方了。

主要是因为上面的 Q-learning 算法更新时会有来自未来的奖励，自然就不断的稀释给前面的行动了。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
def train(n):
    player = NimAI()

    # Play n games
    for i in range(n):
        print(f"Playing training game {i + 1}")
        game = Nim()

        # Keep track of last move made by either player
        last = {
            0: {"state": None, "action": None},
            1: {"state": None, "action": None}
        }

        # Game loop
        while True:

            # Keep track of current state and action
            state = game.piles.copy()
            action = player.choose_action(game.piles)

            # Keep track of last state and action
            last[game.player]["state"] = state
            last[game.player]["action"] = action

            # Make move
            game.move(action)
            new_state = game.piles.copy()

            # When game is over, update Q values with rewards
            if game.winner is not None:
                player.update(state, action, new_state, -1)
                player.update(
                    last[game.player]["state"],
                    last[game.player]["action"],
                    new_state,
                    1
                )
                break

            # If game is continuing, no rewards yet
            elif last[game.player]["state"] is not None:
                player.update(
                    last[game.player]["state"],
                    last[game.player]["action"],
                    new_state,
                    0
                )

    print("Done training")

    # Return the trained AI
    return player

结果

这结果也没法展示，就这么说吧，训练完10000次后，我被 AI 完虐。

不过我学习了一下必胜法就好多了，目前就是谁先手谁输。

思考

智能 or 记忆

不过其实 AI 应该并没有学会必胜法，毕竟我们看看算法就能发现它其实就是把每一步的结果存到字典里了，这叫什么？这叫背公式。

但是我转念一想，如果换我来，在不知道必胜法的情况下，我自己玩一千把，可能也不一定找到必胜法，只能有一种冥冥之中的感觉。

这种感觉是什么呢，也许也是记忆，也许是隐隐感受到了数学公式在里面。

但是就算我能发现必胜法是计算异或值（尼姆和），这也是基于我以前学过数学学过计算机，但是这对于空白一张的 AI 是完全不可能的事情。

除非我提供给它的状态不用 {1, 3, 5, 7} 这样的方式表示，而是直接给出尼姆和，或者给出每个数字的二进制表示，这样也许它才能学到其中的奥秘。

泛化

OK，那假设 AI 已经理解问题了，我们该如何泛化问题呢？

就比如说我现在给 AI 多加一排，变成 {1, 3, 5, 7, 9}，由于有些状态就没在字典里出现过，AI 该怎么选择呢？

我试着写了一下，给大家看看。

  1. 首先找一下这个状态是不是已知的，是的话就不用猜了。
  2. 找不到的话就看看这个未知状态离哪个状态最近，这里的话距离是用异或算的，基本也是变相告诉 AI，尼姆和很重要。
  3. 最后查找离的最近的状态的最好决策，然后让 AI 做出可以和这个最好决策达到相同状态的决策。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
def predict_action(self, state):
    min_distance = int(math.pow(2, 32))
    nearest_state = None
    for state_known, action in self.q.keys():
        if state_known == state:
            return self.choose_action(state, epsilon=False)

        else:
            xor_state = state[0] ^ state[1] ^ state[2] ^ state[3] ^ state[4]
            xor_state_known = state_known[0] ^ state_known[1] ^ state_known[2] ^ state_known[3]

            distance = xor_state ^ xor_state_known
            if distance < min_distance:
                min_distance = distance
                nearest_state = state_known

    predict_action = self.choose_action(nearest_state, epsilon=False)

    for action in Nim.available_actions(state):
        if state[action[0] - action[1]] == state[predict_action[0] - predict_action[1]]:
            return action
    
    return predict_action

给大家看看结果，我没有博弈完，但是我一看到 AI 从第四堆里拿，我就知道泛化成功了，至此 AI 将随意玩任意情况的尼姆游戏。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
Piles:
Pile 0: 1
Pile 1: 3
Pile 2: 5
Pile 3: 7
Pile 4: 9

Your Turn
Choose Pile: 1  
Choose Count: 2

Piles:
Pile 0: 1
Pile 1: 1
Pile 2: 5
Pile 3: 7
Pile 4: 9

AI's Turn
AI chose to take 3 from pile 4.

Piles:
Pile 0: 1
Pile 1: 1
Pile 2: 5
Pile 3: 7
Pile 4: 6

后记

这其实也是我第一次尝试实现强化学习，感觉确实挺好玩的，下一篇可能会让 AI 玩真正的狼人杀了。