前言

又忘写了，赶紧来补，完整代码见 https://github.com/zong4/AILearning。

Optimization

虽然一般都会把优化问题分成下图三类，但是其实如果大家仔细思考一下，就会发现。

优化从本质上来说也是一种 Search，在限制下寻找可行解或者更优解。

OK，先给大家举个例子。

比如说，我们要从下图中找出最高的柱子，但是我们只知道我们目前的柱子和相邻的柱子。

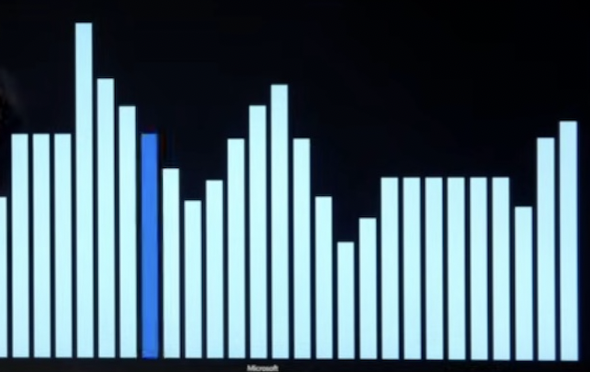
那解这个问题最简单的方法就是比一比相邻的柱子，那边高就往那边爬，那如果都比现在低，那就不走了。

但是这样的话就很容易陷入局部最优解了，那具体如何解决，我们先按下不表，最后再来讲。

Linear Programming

线性规划相信大家肯定不陌生，都是初中的知识了。

一般线性规划都会分成两部分。

  1. 目标函数（花费函数），也就是要优化的东西。

  2. 限制，一般都会有好几条。

    当然了，目标函数其实也可以有好几个，但是我们都会将它转换成一个。

那大家应该发现了相比局部搜索，线性规划中我们的视角是全局的。

Constraint Satisfaction

那这听名字就知道这种问题是找可行解，同样也给大家举个例子。

就下面这个问题，每个圈代表一场考试，旁边的集合就是考试可以被安排的日期，限制条件是相连的节点日期不能相同，问怎么排。

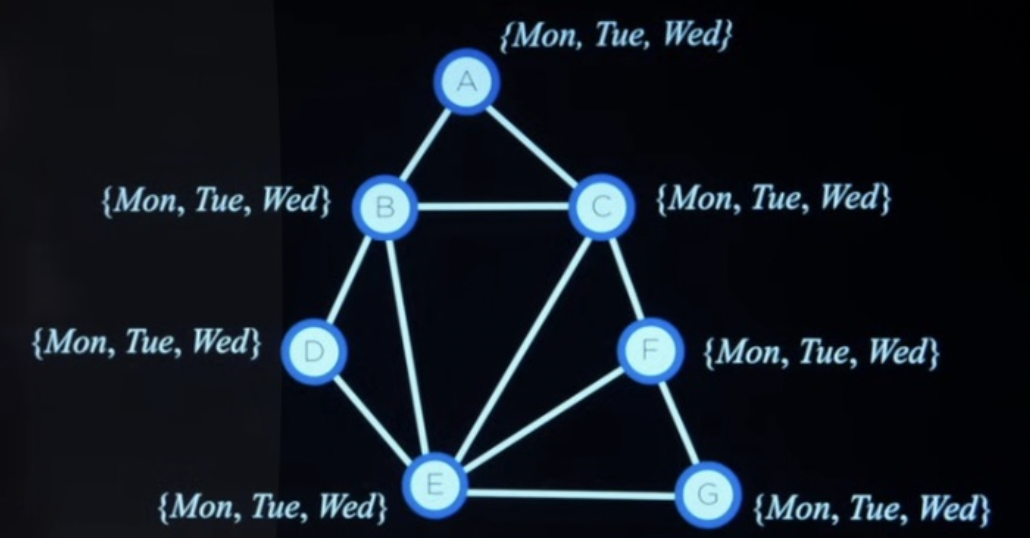
这题目看着挺简单的吧，回溯算法秒解，跟八个皇后问题一样。

那如果更进一步，要求周一的考试尽可能的少呢？

其实还是一样，只要优先填周二和周三就好了。

那如果不算完整，而是只算一个可行解，会陷入局部最优解吗？

那必然是会的，所有的优化问题都有可能陷入局部最优，所以我们最后来讲讲怎么解决。

智能算法

一般我们说智能算法之所以智能是因为它可以逃离局部最优解，有更大的概率进入全局最优解，说白了就是不贪心。

但是本质上智能算法就是比普通算法多了下面这两样。

  1. 保留解并继续探索。
  2. 多个初始状态同时寻找解。

比如常见的退火算法就是保留解，蒙特卡洛模拟和蚁群算法就是多个初始状态。

当然具体算法后续的优化那就各不相同了。

  • 比如退火算法前期更大概率往小的走，后期则趋于平静。
  • 蒙特卡洛模拟则是大范围随机初始状态。
  • 而蚁群算法我记得好像是有个踪迹，就像蚂蚁走路会留下信号，吸引别的蚂蚁。

OK，那除此之外，其实还有很多优化方法，比如说可以先舍弃一些限制寻找，然后再加上，不过这些都要具体问题具体分析了。

填字游戏

这游戏相信大家肯定都不陌生，小时候都在杂志或者报纸上玩过。

不过这里填的词不是根据要回答的问题来的，而是从一堆词里选。

给大家举个例子，想想怎么来解，假设有下面这样的谜题。

要求从 {one, two, three, four, five, six, seven, eight, nine, ten} 中选词。

  1. 首先我们可以将词表中不符合要求的词剔除（长度不对），然后再按照长度分成子集，{one, two, six, ten}，{three, seven, eight}，{four, five, nine}。
  2. 然后从可选词最少的空开始填，这里我们就会先填 three。
  3. 填完之后填和它有相同字母的空，这里会填 one，但是字母对不上，所以继续往下找到 two，另一边的话就会发现找不到，就会回溯，将 three 改成 seven。
  4. 然后重复第三步，直至全部填完或者遍历所有可能。

那最后我们就会有如下解。

后记

其实即使是智能算法也会陷入局部最优，这是很正常的事情了，所以才会有数学建模，需要大家去针对性的改进智能算法。

那用 AI 呢？或者更确切的说用 Machine Learning 呢，也就是用数据集来优化。

怎么说呢，也许结果会更好，也许会更差，这取决于你的数据集和模型。

不过我们还有更进一步的强化学习，对抗式人工智能，这也许才能大大提高模型寻找最优解的可能性（但也不是所有问题都可以）。