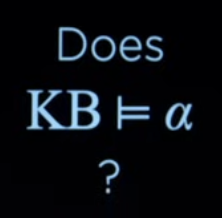前言

完整代码见 https://github.com/zong4/AILearning。

定义

所谓的 Knowledge 就是指逻辑推理。

就像经典的苏格拉底三段论一样。

结构

一个完整的可以分成什么呢？

Proposition Symbols

这里的 Symbols 是指一句完整的有主谓宾的句子。

看一下代码吧，这块感觉没什么好讲的，不懂再说吧。

class Sentence:
    def evaluate(self, model):
        raise NotImplementedError
    
    def formula(self):
        return ""
    
    def symbols(self):
        return set()
    
    @classmethod
    def validate(cls, sentence):
        if not isinstance(sentence, Sentence):
            raise TypeError("must be a logical sentence")
        
    @classmethod
    def parenthesize(cls, s):
        p = re.compile(r"\s*([()])\s*")
        return p.sub(r" \1 ", s).strip()
    
class Symbol(Sentence):
    def __init__(self, name):
        self.name = name
        self.true = 0
        self.false = 0
    
    def __eq__(self, other):
        return isinstance(other, Symbol) and self.name == other.name
    
    def __hash__(self):
        return hash(("symbol", self.name))
    
    def __repr__(self):
        return self.name
    
    def evaluate(self, model):
        try:
            return bool(model[self.name])
        except KeyError:
            raise Exception(f"variable {self.name} not in model")
    
    def formula(self):
        return self.name
    
    def symbols(self):
        return {self.name}

Logic Connectives

这也是逻辑推理的核心，基本的逻辑主要是以下五个。

Not
And
Or
Implication
Biconditional

需要注意的是，这不像大学里学的数字逻辑，没有异或也没有同或，取而代之的是 Implication（推导）和 Biconditional（充分必要条件）。

举个例子，如果今天下雨（P），我就不出门（Q），这样一句话就可以表示为 $P\rightarrow Q$，它的是非表如下。

可以看出，只有当条件为真，结果为否是，$P\rightarrow Q$ 才等于 false。

再来，如果且只有（if and only if）今天下雨（P），我才不出门（Q），这样一句话就可以表示为 $P\leftrightarrow Q$，它的是非表如下。

可以看出这就和上面的单向箭头有区别了。

给大家放了 Not 和 And 的实现代码，剩下三个就自己来实现吧。

class Not(Sentence):
    def __init__(self, operand):
        Sentence.validate(operand)
        self.operand = operand
    
    def __eq__(self, other):
        return isinstance(other, Not) and self.operand == other.operand
    
    def __hash__(self):
        return hash(("not", hash(self.operand)))
    
    def __repr__(self):
        return f"(not {self.operand})"
    
    def evaluate(self, model):
        return not self.operand.evaluate(model)
    
    def formula(self):
        return "¬" + Sentence.parenthesize(self.operand.formula())
    
    def symbols(self):
        return self.operand.symbols() 
    
class And(Sentence):
    def __init__(self, *conjuncts):
        for conjunct in conjuncts:
            Sentence.validate(conjunct)
        self.conjuncts = list(conjuncts)
    
    def __eq__(self, other):
        return isinstance(other, And) and self.conjuncts == other.conjuncts
    
    def __hash__(self):
        return hash(("and", tuple(hash(conjunct) for conjunct in self.conjuncts)))
    
    def __repr__(self):
        conjunctions = ", ".join(str(conjunct) for conjunct in self.conjuncts)
        return f"(and {conjunctions})"
    
    def evaluate(self, model):
        return all(conjunct.evaluate(model) for conjunct in self.conjuncts)
    
    def formula(self):
        conjunctions = "(" + " ∧ ".join(Sentence.parenthesize(conjunct.formula()) for conjunct in self.conjuncts) + ")"
        return Sentence.parenthesize(conjunctions)
    
    def symbols(self):
        return set().union(*(conjunct.symbols() for conjunct in self.conjuncts))

Model

这里的 Model 不是模型，而是指一个存在所有 Symbols 的空间。可以理解为一个 Model 就是是非表里的一行，所有 Model 就构成了是非表。

Knowledge Base

这个是所有已经条件的集合。

Entailment

可以理解为所有 Model 的共识，这也是需要 AI 来回答的问题。

也就是说当我给出所有的 Knowledge Base，$\alpha$ 这个 Symbol 所代表的事情是否一定为真。

Inference

没什么好说的，就是上图的 $\alpha$，也就是要求证的事情。

Model Checking

这就是来验证 Inference 对不对了，需要注意的是，只有当 KB 为 true 时，才需要检查 Inference 是不是 true。

考虑下图的 Entailment，只有绿色那一种情况下 KB 是真的，因此只看那一条，可以发现 R 是 true，所以可以完成这个推论。

看一下代码，可以发现是递归式的，即需要把所有 Symbol 都打上 true 或者 false，也就是创建一个完整的新 Model后，才能判断 Entailment。

def model_check(knowledge, query):
    def check_all(knowledge, query, symbols, model):
        if not symbols:
            if knowledge.evaluate(model):
                if query.evaluate(model):
                    query.true += 1
                else:
                    query.false += 1
                return query.evaluate(model)
            return True
        
        remaining = symbols.copy()
        p = remaining.pop()
        return (check_all(knowledge, query, remaining, {**model, **{p: True}}) and
                check_all(knowledge, query, remaining, {**model, **{p: False}}))
    
    symbols = knowledge.symbols().union(query.symbols())

    return check_all(knowledge, query, symbols, model={})

结果

OK，来一个实例。

rain = Symbol("rain") # It's raining.
hagrid = Symbol("hagrid") # Zong will visit Hagrid.
dumbledore = Symbol("dumbledore") # Zong will visit Dumbledore.

knowledge = And(
    Implication(rain, hagrid), # If it's raining, then Zong will visit Hagrid.
    Or(hagrid, dumbledore), # Zong will visit Hagrid or Zong will visit Dumbledore.
    Not(And(hagrid, dumbledore)), # Zong will not visit both Hagrid and Dumbledore.
    hagrid, # Zong will visit Hagrid.
)

inference = rain

print(knowledge.formula()) # Should be (rain => hagrid) ∧ (hagrid ∨ dumbledore) ∧ ¬(hagrid ∧ dumbledore) ∧ hagrid

symbols = [rain, hagrid, dumbledore]
for symbol in symbols:
    if model_check(knowledge, symbol):
        print(f"{symbol}: Yes")
    else:
        prosibilities = symbol.true / (symbol.true + symbol.false)
        if prosibilities == 0:
            print(f"{symbol}: No")
        else:
            print(f"{symbol}: {prosibilities * 100:.2f}%")

KB 第一句是一句推导，如果下雨，那么 Zong 会去拜访 Hagrid，第二句是 Zong 一定会去拜访一个，第三句是说 Zong 一次只会拜访一个（如果没有这句就不能得出一定不会去拜访 Dumbledore）。

其中可以看到正如之前所说，先创建 Symbols，然后通过逻辑符组成 KB，最后就可以检查在所有可能情况下，各个 Symbol 为真的概率，当然你也可以让他直接来给出结论，最后的输出如下。

( rain => hagrid ∧ ( hagrid ∨ dumbledore ) ∧ ¬ ( hagrid ∧ dumbledore ) ∧ hagrid )
rain: 50.00%
hagrid: Yes
dumbledore: No

其中，第一行是 KB 的公式。

通过结果可以看出 Zong will visit Hagrid. 是肯定会发生的，Zong will visit Dumbledore. 是肯定不会发生的，下雨是一件不相关的事情（因为没说只有下雨才……），所以是 50%。

改进

其实看到 Model Checking 的算法，就可以预见在很多 Symbols 的情况下计算时间会几何飙升，所以简化 Symbols 很重要，让它数量越少越好。

怎么简化呢，其实大家如果自己写了 Implication 和 Biconditional 这两个逻辑的实现代码就会发现，这两个玩意是可以用前三个来表示的，就像异或也可以用简单的逻辑来表达一样，这就是简化的关键。

想象一下，将所有逻辑都只有 Not 和 Or 来表达，然后再通过那些合并简化的公式，就自然而然可以让 Symbols 的数量减少，从而降低运行时间。

后记

其实通过以上的操作就能让AI具备推理能力了，因为人类也就是这样做的，再加上 NLP（自然语言处理），AI 就可以不用人类来分割语言了。