前言

完整代码见 https://github.com/zong4/AILearning。

定义

所谓 Search 就是寻找最优解。

生活中的话像导航，或者之前比较火的 AlphaGo 下围棋都算，我们就从比较有代表的迷宫开始。

Maze

顺带一提，之前做雅思，好像 amaze 就是从 maze 延申出来的。

每一个 Maze，或者说每一个 Search 问题都能被分成以下几个部分。

Agent

或者说 Player，如果是导航，那 Agent 就是你自己，如果是博弈游戏，那就是参与游戏的每个人。

Initial State

同样的，如果是导航那就是你的起点，如果是围棋，那就是空棋盘。

Actions

被规则允许的所有 Action。

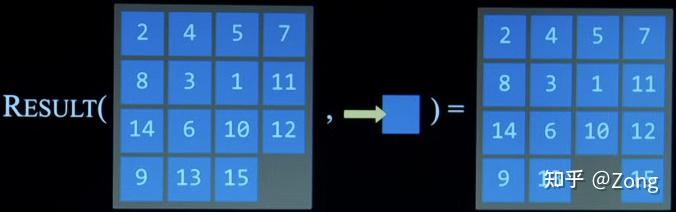
Transition Model

1
2
3
def Result(State, Action):
    ...
    retun state

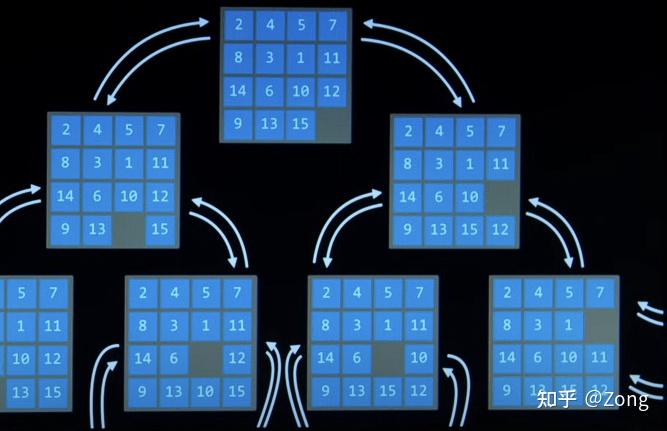
State Space

没什么好说的，状态转移图。

可以被简化成有向图。

Goal Test

没什么好说的，不然连解出来了都不知道。

Path Cost Function

不同问题中的 Path Cost 是不一样的，可能是时间，可能是距离，也可能是单位1（围棋每一手的成本都是一样的），也可以是预测的未来成本。

Solution

既然是寻找解，肯定要知道解是什么，或者说目标状态是怎么样的。

对于单人问题，解自然是满足你的需求或者说达成你的目标。

但是多人问题就不一样了，以围棋举例，就是输赢平三种解。

Optimal Solution

单人问题很简单，最契合你的需求的就是最优解。

多人问题就比较复杂了，如果是合作，那很明显就是一起获得更多的分，如果是零和博弈，那就是让对方获得的分更少，而不是让自己获得的分更多，其他博弈的话也基本是让自己的分更多。

Data Structure

没什么好说的，用节点就好了。

1
2
3
4
5
6
class Node():
    def __init__(self, state, parent, action, cost):
        self.state = state # 当前状态
        self.parent = parent # 父亲状态
        self.action = action # Transition Model 里的 action
        self.cost = cost # 总成本

Algorithm

这两个么没什么好说的了就，直接看代码吧。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
class StackFrontier():
    def __init__(self):
        self.frontier = []

    def add(self, node):
        self.frontier.append(node)

    def contains_state(self, state):
        return any(node.state == state for node in self.frontier)

    def empty(self):
        return len(self.frontier) == 0

    def remove(self):
        if self.empty():
            raise Exception("empty frontier")
        else:
            node = self.frontier[-1]
            self.frontier = self.frontier[:-1]
            return node
        
class QueueFrontier(StackFrontier):
    def remove(self):
        if self.empty():
            raise Exception("empty frontier")
        else:
            node = self.frontier[0]
            self.frontier = self.frontier[1:]
            return node
        
class Maze():
    def __init__(self, filename):
        ...
    def print(self):
        ...

    def neighbors(self, state):
        ...
    
    def solve(self):
        start = Node(state=self.start, parent=None, action=None, cost=0)
        frontier = QueueFrontier()
        frontier.add(start)

        self.explored = set()

        while True:
            if frontier.empty():
                raise Exception("no solution")

            node = frontier.remove()
            self.explored.add(node.state)

            if node.state == self.goal:
                actions = []
                cells = []
                while node.parent is not None:
                    actions.append(node.action)
                    cells.append(node.state)
                    node = node.parent
                actions.reverse()
                cells.reverse()
                self.solution = (actions, cells)
                return

            for action, state in self.neighbors(node.state):
                if not frontier.contains_state(state) and state not in self.explored:
                    child = Node(state=state, parent=node, action=action, cost=node.cost + 1)
                    frontier.add(child)

Revised Approach

这个也没什么好说的，就是因为可能是带环图，所以要有一个状态集存放已经探索过的状态。

Greedy Best-first Search（贪婪算法）

由于 DFS 只是随机转移，不考虑未来到达解还需要多少成本，所以有时候找到的不是最优解，而 BFS 占用空间又过大，所以需要优化 DFS。

贪婪算法每次都往 Estimated Cost to Goal 最低的状态过渡（此时 Node 中的 cost 就应该是 Estimated Cost to Goal 而不是 Sum Cost，因为只要找到就必然是最优解）。

在迷宫游戏中，每个状态到解的成本的预测值就是 Agent 此时到解的曼哈顿距离（dx + dy）。

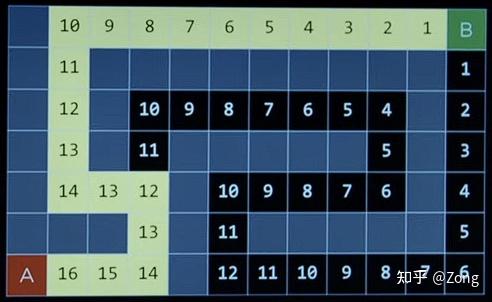
当然了贪婪算法还是有问题的，在如下图中使用贪婪算法就依然找不到最优解，因为没有考虑到 Cost to Reach Node。

所以目前的最终 cost = cost to reach node + estimated cost to goal($\geq$ 0)。

图中的数字是预测的总 cost = cost to reach node + estimated cost to goal
值得注意的是，即使是 A 算法也不是一定能找到最优解的（因为找不到完美的的估价函数）*，但是那些就得视情况做针对性的优化了。

后记

写的不少了，不知道大家觉得难度怎么样（这一篇应该算比较简单的了）。

下一篇会讲零和博弈游戏。